计算机图形学入门IX

Ray Tracing 1 (Whitted-Style Ray Tracing)

一、概述

1. 引入光线追踪的原因是光栅化很难做出效果好的全局效果，比如软阴影、全局照明
2. 光线追踪也有一定的问题，最严重的问题是非常慢，光栅化常用于实时场景，光线追踪则更多应用于离线场景，因此两者并无替代关系而是相互独立的

二、基础光线追踪算法

1. 关于光线的三个性质(理论)
   • 光沿直线传播
   • 光线之间不会发生碰撞
   • 光线一定是从光源发射出来在环境中经过不断的反射到达观测点(人眼/摄像机)
2. 点观察模型(Pinhole Camera Model)
   
3. Whitted-Style 光线追踪(递归)：将反射折射等全部累加起来得到最终的视觉图
   
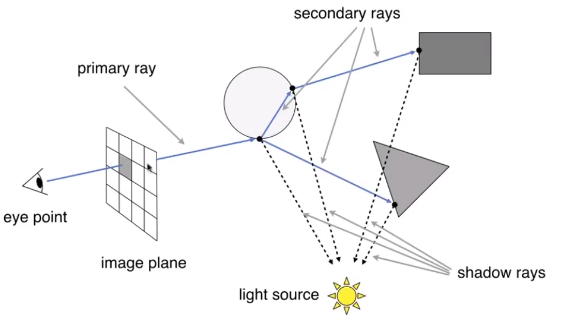
   • shadow rays 用于判断可见性
   • primary ray 初始光线
   • secondary ray 折射反射后的次级光线
4. 光线和物体表面的交点
   
   
   分别设出光线与圆的方程，联立解出未知量 $t$ (传播时间)判断与圆的交点情况，将解出的$t$代回到光线方程中即可得到交点的具体数值
   • 封闭图形内射出的光线与图形的交点一定是奇数个(同理可以推广到三维情况下)
   • 在图形学中通常忽略平行这种特殊情况(例如光线恰好经过某一平面)
5. 特殊到光线与三角形的交点：通常先求出光线与三角形所在平面的交点，然后判断该交点是否在三角形内
   
   
6. Moller Trumbore Algorithm：上述过程还是较为复杂，为了直接判断交点是否在三角形内，于是有了利用重心坐标求解的Moller Trumbore 算法($b1,b2,1-b1-b2$分别为重心坐标)
   

三、加速线面求交流程

1. 包围盒(Bounding Volumes)：用简单的物体包围复杂的物体那么对于光线来说，如果与包围盒都没有交点的话就不用说与被包围的物体了
2. Axis-Aligned Bounding Box(AABB)：轴对齐包围盒
3. 以二维情况为例，可以计算出光线出入x,y两个对面的时间以及交点，求交集即可得到最终光线与盒子的交点与时间
   
4. 推广到三维情况就是x,y,z三个对面，同理光线同时进入三个对面则称光线进入包围盒，光线射出任意一个对面则称光线离开包围盒
   • $t_{enter} = max{t_{min}}$
   • $t_{exit} = min{t_{max}}$
   • 如果 $t_{enter} < t_{exit}$，则称光线在盒子中停留过一段时间，反之则称光线未进入盒子
   • 如果 $t_{exit}<0$，显然不存在交点
   • 如果 $t_{enter} < 0 \ &\ t_{exit}>=0$，可以想象到光在盒子里出发，则一定有交点
     综上所述，光线与AABB模型有交点当且仅当$t_{enter} < t_{exit} \ &&\ t_{exit}>=0 $

(下接 计算机图形学入门X)