计算机图形学入门XIV

Materials and Appearances

一、Material == BRDF

二、Diffuse Material

重新定义漫反射系数：一个点不发光同时也不吸收光，那么它会将所有光反射出去

$$\begin{aligned} L_o(w_o) & = \int_{H^2}f_rL_i(w_i)cos\theta_idw_i \\ &=f_rL_i\int_{H^2}(w_i)cos\theta_idw_i \\ &=\pi f_rL_i \end{aligned}$$ $$f_r = \frac{\rho}{\pi} \quad \rho=albedo(color)$$

三、Specular Reflection

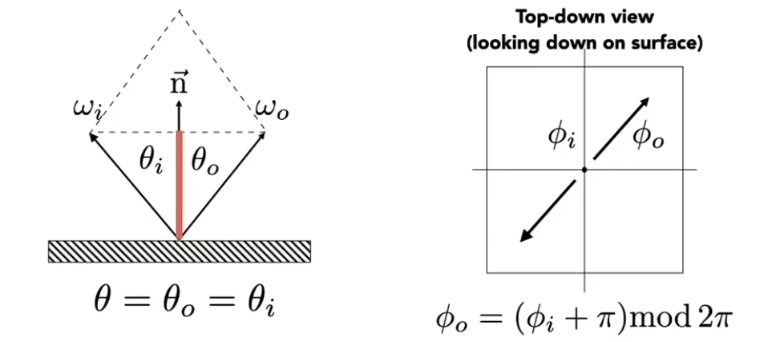
$$w_o+w_i = 2cos\theta \vec n=2(w_i \cdot \vec n)\vec n \\ w_o = -w_i+2(w_i \cdot \vec n)\vec n$$

Tip：图中$\theta$为出入射角，$\phi$为出入射角的平面角

四、Specular Refraction

1. Snell’s Law：折射角度取决于出入射光的Z折射率(IOR:index of refraction)

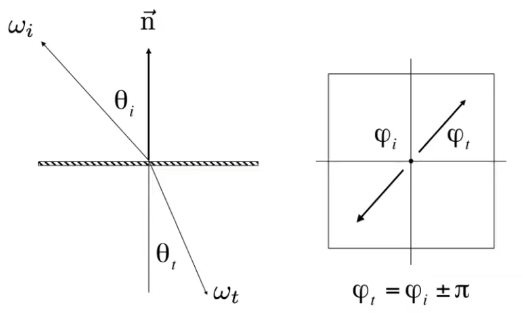
1. Law of Refraction:

   $$\begin{aligned} \eta_isin\theta_i & = \eta_tsin\theta_t \\ cos\theta_t & = \sqrt{1-sin^2\theta_t} \\ & = \sqrt{1- {\left( \frac{\eta_i}{\eta_t} \right)}^2 sin^2\theta_i} \\ & = \sqrt{1- {\left( \frac{\eta_i}{\eta_t} \right)}^2 \left( 1-cos^2\theta_i \right)} \end{aligned}$$

   这个式子也可以看出全反射的条件：

   $${1- {\left( \frac{\eta_i}{\eta_t} \right)}^2 \left( 1-cos^2\theta_i \right)} < 0$$

2. Fresnel Reflection/Term(菲涅耳项)：反射率取决于入射角(以及光的偏振度)。
   

五、Microfacet Material

1. 微表面模型：物体表面是粗糙的，但从远处看基本是平的，因此认为其在远处看是粗糙(材质)的平面，每一个表面的元素可以看做是镜面，每个微表面有自己的法线。
2. Microfacet BRDF：可以用微表面的法线分布来表示材质的粗糙程度
   
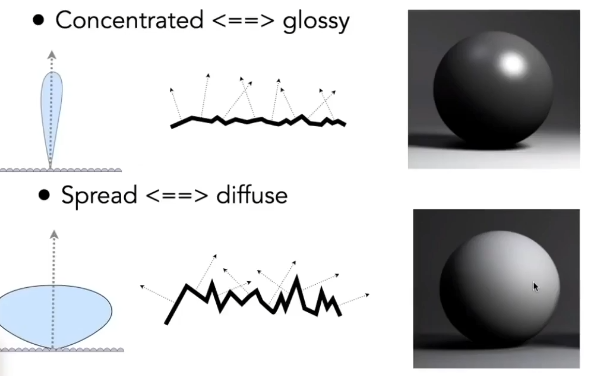
3. Isotropic/Anisotropic：各向同性/各向异性
4. 各向同性(Isotropic)材质：表现为表面不存在方向性或方向性很弱
   

六、Properties of BRDFs

1. 能量非负性 $$f_r(w_i\rightarrow w_r)\ge 0$$
2. 线性性质：指每个部分可以单独拿出来进行计算最后求和
3. 可逆性：交换出入射方向得到的BRDF是相同的 $$f_r(w_i\rightarrow w_r) = f_r(w_r\rightarrow w_i)$$
4. 能量守恒

七、Measuring BRDFs

1. Image-Based BRDF Measurement：选中一个着色点，不断改变光源的入射光线和摄像机的出射光线，遍历测量。
   

(下接 计算机图形学入门XV)