计算机图形学入门XVIII

Animation(simulation)

一、概述

1. Keyframe Animation：关键帧动画
   • Animator(eg:lead animator) 创建关键帧
   • Assistant(other person or computer) 创建中间帧
     中间值通过插值计算得到
2. Physical Simulation：物理仿真模拟
3. Mass-Spring System：质点弹簧系统
   • 结构弹簧(struct spring)
   • 剪应弹簧(shear spring)
   • 弯曲弹簧(bend spring)
   • 阻尼系数(damp)
4. Particle System：粒子系统
   对于动画中的每一帧：
   • 如果需要，创建新的粒子
   • 计算每个粒子的受力
   • 改变每个粒子的速度和位置
   • 如果需要，移除死亡粒子
   • 渲染粒子
5. 正运动学(Forward Kinematics)：描述一种骨骼系统来模拟人体
   • Pin(1D rotation)
   • Ball(2D rotation)
   • Prismatic joint(translation)
6. 联动计算
   

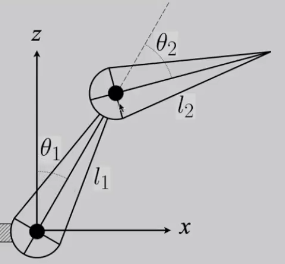
$$p_z = l_1 cos(\theta_1) + l_2 cos(\theta_1 + \theta_2) \\\\ p_x = l_1 sin(\theta_1) + l_2 sin(\theta_1 + \theta_2)$$

1. 逆运动学(Inverse Kinematics)：给定一个确定运动，如何计算运动过程

2. Rigging：一种更高级别的控制，它允许对姿态、形变、表情等进行直观的修改

3. Blend Shapes：表情和骨骼动画混合

4. Motion Capture：动作捕捉

二、

1.Single Particle Simulation

1. 欧拉方法(线性模型) $$x^{t+\Delta t} = x ^ t + \Delta t \dot x^t \\\\ \dot x^ {t + \Delta t} = \dot x ^ t + \Delta t \ddot x^t$$ 该方法稳定性较差，误差会随着时间递增
2. 中点法(平方级模型) $$x_{mid} = x(t) + \Delta t/2 \cdot v(x(t),t) \\\\ x(t + \Delta t) = x(t) + \Delta t \cdot v(x_{mid},t)$$

3. 修正后的欧拉方法

   $$x^{t+ \Delta t} = x ^ t + \frac{\Delta t}{2}(\dot x ^ t + \dot x ^{t+\Delta t}) \\\\ \dot x ^ {t + \Delta t} = \dot x ^ t + \Delta t \ddot x ^ t \\\\ x ^ {t + \Delta t} = x ^ t + \Delta t \dot x ^ t + \frac{(\Delta t)^2}{2} \ddot x ^ t$$

4. 隐式欧拉方法

   $$x ^ {t + \Delta t} = x ^ t + \Delta t \dot x ^ {t + \Delta t} \\\\ \dot x ^ {t + \Delta t} = \dot x ^ t + \Delta t \ddot x ^ {t + \Delta t}$$

5. 龙格库塔方法(Runge-Kutta)
   详见数值分析课本XD

6. 刚体模拟(Rigid Body Simulation)

   $$\frac{d}{dt} \begin{pmatrix} X\\\\ \theta\\\\ \dot X\\\\ \omega \end{pmatrix} = \begin{pmatrix} \dot X\\\\ \omega\\\\ F/M\\\\ \Gamma / I \end{pmatrix}$$
   • $X$:positions
   • $\dot X$:acceleration
   • $\theta$:rotation angle
   • $\omega$:angular velocity
   • $F$:force
   • $\Gamma$:torque
   • $I$:momentum of inertia

2.Fluid Simulation

1. 先给出一个简单的模型：将整个水体看做是数量众多的不可压缩的刚体小球组成，当水体某处的小球密度发生改变，则考虑如何使之恢复，这一过程就是在模拟流体流动(梯度下降法(gradient descent))
2. 对于模拟大型集合物体的两种不同方法：
   • Lagrangian Approach(拉格朗日法/质点法)
   • Eulerian Approach(欧拉方法/网格法)

课程到此结束，再次感谢闫老师，GAMES101作为入门课程，为我们讲解了图形学的众多研究方向，至于之后到底要向那个方向深入研究，全凭个人喜好，望坚持~

完结撒花~~