FABIK算法

Unity中实现反向动力学算法FABIK

该算法主要运用于机器人仿真模拟过程中实现机械臂的运动模拟

一、FABRIK算法

1.模型抽象与化简

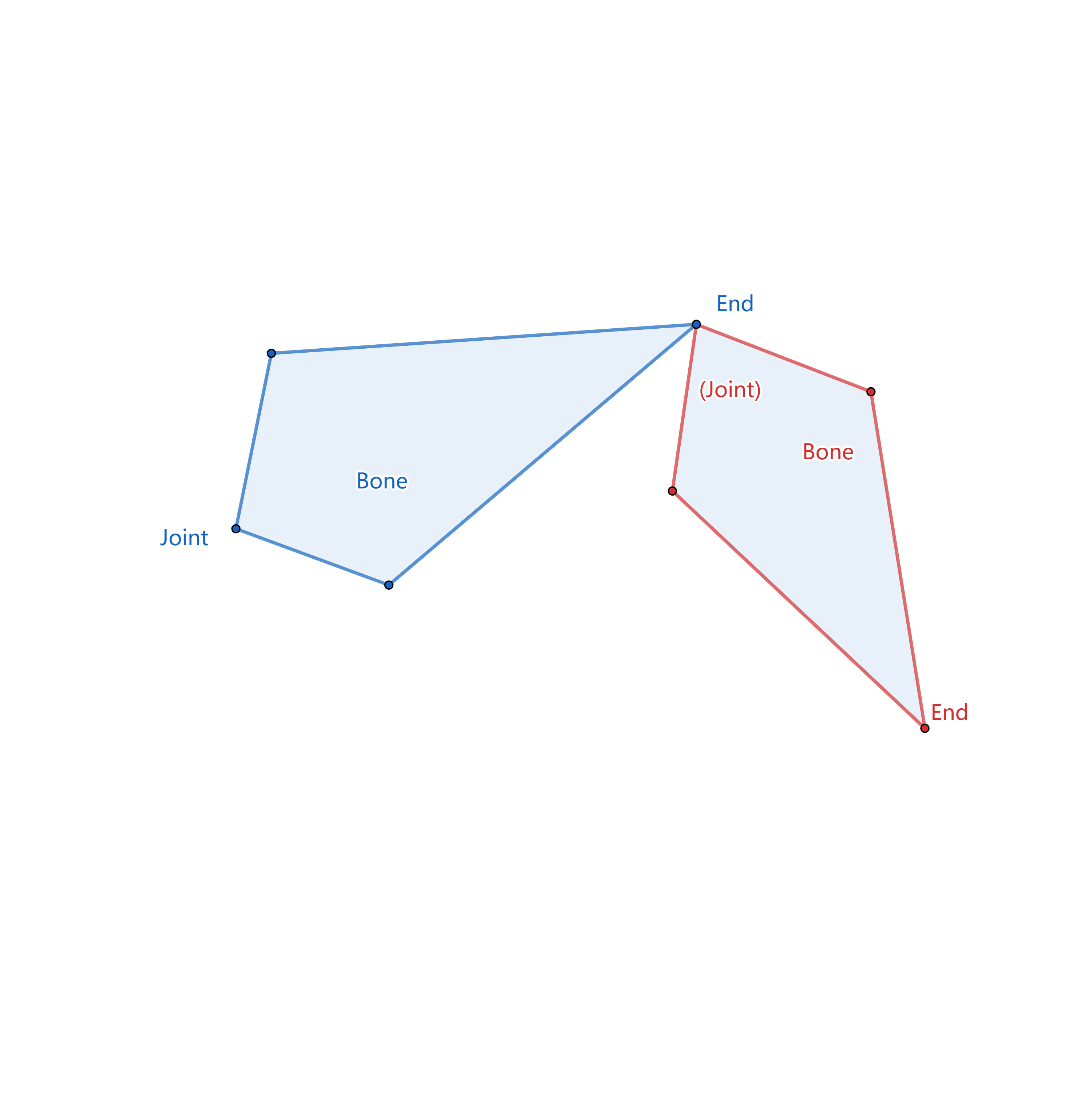
以工业机器人中的机械臂为模型，可以将其抽象为一个拥有关节的骨骼系统，该系统有若干骨骼：

骨骼(Bones) 机器人的每一段机械臂
关节(Joint) 骨骼的起点
末端(End) 骨骼的终点
整个机械臂可以抽象成为一条骨链
骨链的起点称为根节点
骨链的终点称为叶节点
目标(Target)是末状态要到达的位置
轴(Pole)是以骨链为整体的旋转轴

2.算法详解

原理是首先计算当前末端执行器位置与期望位置之间的距离，然后使用前向和后向到达算法将该距离分布到机械臂的各个部分。前伸算法从机械臂的底部开始，向末端执行器移动，调整每个关节的位置，减少相邻关节之间的距离。后向到达算法从末端执行器开始，向基座移动，调整每个关节的位置，减少相邻关节之间的距离。重复这两个步骤，直到获得所需的末端执行器姿态。算法分为两种情况：

Target在骨链所及范围之外：也就是根关节与Target之间的距离大于整个骨链总长的情况。这种情况下整个骨链是完全伸直的，只需要确定跟关节与Target的方向向量，通过计算各个Bone的长度，确定它们在这个方向上新的位置即可
Target在骨链所及范围之内：分为 Forward Reaching 与 Backward Reaching 两个阶段
- FR: 将叶节点的末端移动到Target的位置，根据它与其父节点之间骨骼的长度，在它与父节点的连线上找到父关节新位置，完成节点的移动，以此类推，直到根关节也完成移动
- BR: 此时我们可以看到根关节移动到了一个新位置，但在实际模型中，根节点往往是固定点。此时我们将根节点重新移动至其初始位置，然后根据根节点和它子节点之间的骨骼长度，在根节点与它子节点的连线上找到这个关节的新位置，然后移动，以此类推，直到确定叶节点的位置。
  完成这样一个来回之后，我们发现根节点偏离了Target的位置，剩下的步骤就是重复FR与BR，直到叶节点与Target之间的距离小于一个阈值，迭代就算完成。下面图示展示了这一过程：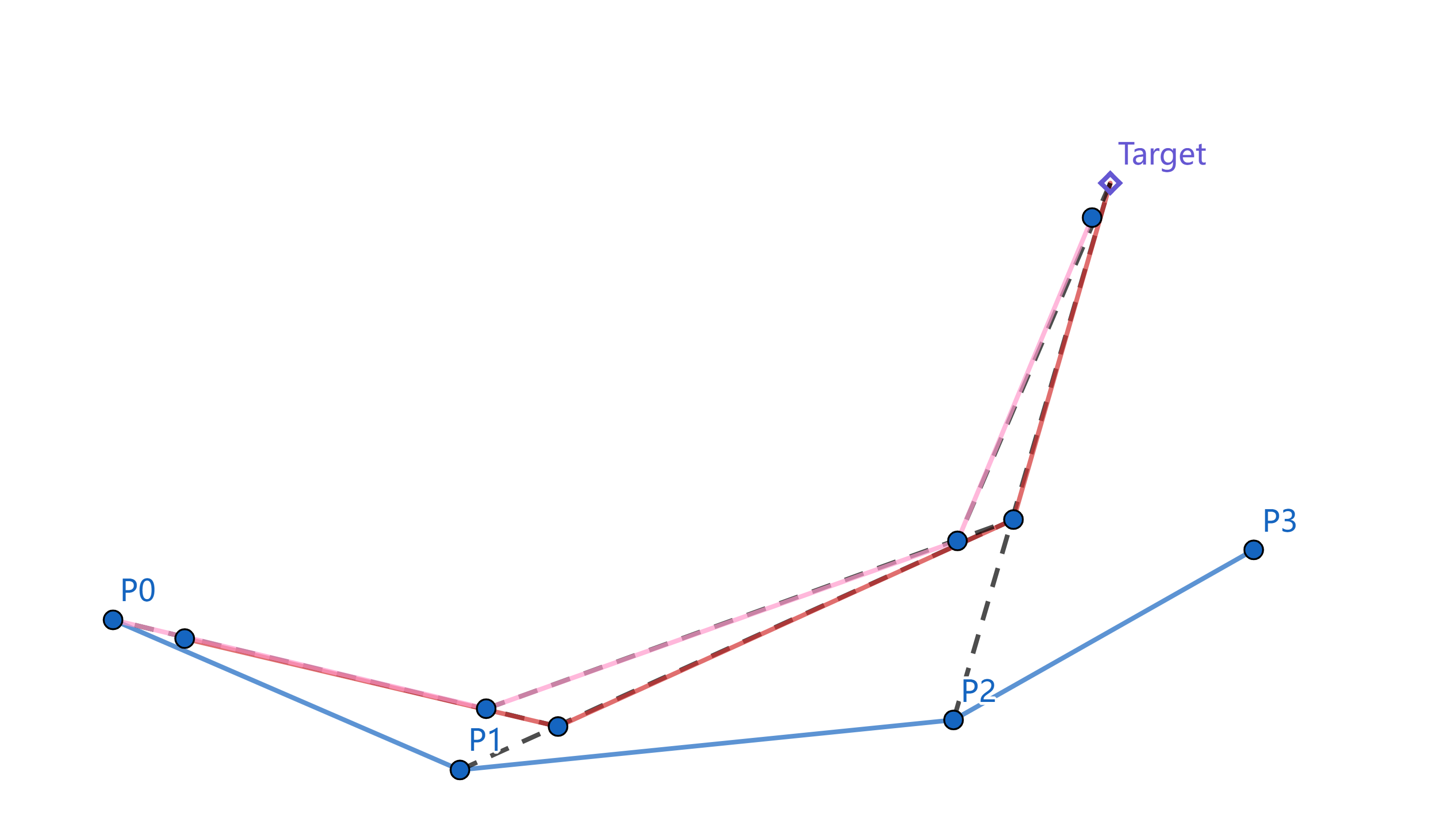

二、Unity实现

1.属性

// 骨链长度(Bones数量)
public int ChainLength;
// 目标位置
public Transform Target;
// 骨链轴的位置
public Transform Pole;
// 迭代次数(收敛约束)
public int Iterations;
// 距离阈值(收敛约束)
public float Delta;

// 根节点的位置
protected Transform Root;
// 骨骼坐标数组
protected Transform[] Bones;
// 骨骼长度数组(或者说关节之间的距离)
protected float[] BonesLength;
// 骨骼总长度
protected float CompleteLength;
// 当前骨骼坐标数组
protected Vector3[] Positions;
// 骨骼向量数组
protected Vector3[] StartDirectionSucc;
// 初始时Bone的Rotation数组
protected Quaternion[] StartRotationBone;
// 初始时Target的Rotation
protected Quaternion StartRotationTarget;

2.坐标计算函数

获取某一节点在根节点坐标系中的位置

private Vector3 GetPositionRootSpace(Transform current)
{
    if (Root == null)
        return current.position;
    else
        return Quaternion.Inverse(Root.rotation) * (current.position - Root.position);
}

这段代码中，Quaternion.Inverse(Root.rotation)表示Root的旋转四元数的逆，即将Root的旋转反向；current.position - Root.position表示从Root的位置到current的位置的向量。将这两个量相乘，实际上是将向量从Root的局部坐标系转换为世界坐标系

具体来说，如果我们有一个点current，它在Root的局部坐标系中的坐标是p_local，则该点在世界坐标系中的坐标p_world可以用以下公式计算：

1	`p_world = Root.position + Quaternion.Inverse(Root.rotation) * (p_local - Root.position)`

其中，Root.position表示Root在世界坐标系中的位置，Quaternion.Inverse(Root.rotation)表示Root的旋转四元数的逆。该公式的含义是，首先将p_local转换为一个相对于Root局部坐标系的向量，然后通过将其乘以Root的旋转四元数的逆，将该向量从局部坐标系转换为世界坐标系，并加上Root在世界坐标系中的位置，得到该点在世界坐标系中的坐标

Tips: Transform.position拿到的都是世界坐标该方法返回的是计算出的该节点的根节点坐标系的坐标

设置某一节点在根节点坐标系中的位置

private void SetPositionRootSpace(Transform current,Vector3 position)
{
    if (Root == null)
        current.position = position;
    else
        current.position = Root.rotation * position + Root.position;
}

四元数与向量相乘表示该向量按照这个四元数进行旋转后得到新的向量，加上根节点坐标就求可以将cur的位置移动到传入的position位置

获取某一节点在根节点坐标系中的旋转

private Quaternion GetRotationRootSpace(Transform current)
{
    if (Root == null)
        return current.rotation;
    else
        return Quaternion.Inverse(current.rotation) * Root.rotation;
}

与position方法类似

设置某一节点在根节点坐标系中的旋转

private void SetRotationRootSpace(Transform current,Quaternion rotation)
{
    if (Root == null)
        current.rotation = rotation;
    else
        current.rotation = Root.rotation * rotation;
}

与position方法类似

3.初始化

初始化数组

Bones = new Transform[ChainLength + 1];
Positions = new Vector3[ChainLength + 1];
BonesLength = new float[ChainLength];
StartDirectionSucc = new Vector3[ChainLength + 1];
StartRotationBone = new Quaternion[ChainLength + 1];

查找根节点

Root = transform;
for (var i = 0; i <= ChainLength; i++)
{
    if (Root == null)
        throw new UnityException("The chain value is longer than the ancestor chain!");
    Root = Root.parent;
}

Tips:该脚本挂在叶节点上，所以通过这种方式查找根节点

初始化Target

if (Target == null)
{
    Target = new GameObject(gameObject.name + " Target").transform;
    SetPositionRootSpace(Target, GetPositionRootSpace(transform));
}
StartRotationTarget = GetRotationRootSpace(Target);

如果Target存在，则将Target移动到根节点坐标系下叶节点的位置
然后获取系统初始时Target的Rotation(StartRotationTarget)

初始化骨骼数据

var current = transform;
CompleteLength = 0;
for (var i = Bones.Length - 1; i >= 0; i--)
{
    Bones[i] = current;
    StartRotationBone[i] = GetRotationRootSpace(current);
    if (i == Bones.Length - 1)
    {
        StartDirectionSucc[i] = GetPositionRootSpace(Target) - GetPositionRootSpace(current);
    }
    else
    {
        StartDirectionSucc[i] = GetPositionRootSpace(Bones[i + 1]) - GetPositionRootSpace(current);
        BonesLength[i] = StartDirectionSucc[i].magnitude;
        CompleteLength += BonesLength[i];
    }
    current = current.parent;
}

主要计算结点之间的向量，如果是叶节点，则是Target-current，其他结点则是子节点-父节点，获得向量后Vector.magnitude获取向量长度，即骨骼长度

4.IK模拟

初始化数据

for (int i = 0; i < Bones.Length; i++)
    Positions[i] = GetPositionRootSpace(Bones[i]);
var targetPosition = GetPositionRootSpace(Target);
var targetRotation = GetRotationRootSpace(Target);

第一种情况：Target在骨链所及范围之外

if ((targetPosition - GetPositionRootSpace(Bones[0])).sqrMagnitude >= CompleteLength * CompleteLength)
{
    // direction是方向向量，所以normalized
    var direction = (targetPosition - Positions[0]).normalized;
    for (int i = 1; i < Positions.Length; i++)
        Positions[i] = Positions[i - 1] + direction * BonesLength[i - 1];
}

初始化时已经将Target位置移到了叶节点的末端，只需要判断Target到根关节的距离与骨骼总长度即可，如果符合条件，各个关节在两点连线上依次排列(伸直骨链)即可得到最终结果

第二种情况：Target在骨链所及范围之内

for (int iteration = 0; iteration < Iterations; iteration++)
{
    // Backward Reaching
    for (int i = Positions.Length - 1; i > 0; i--)
    {
        if (i == Positions.Length - 1)
            Positions[i] = targetPosition;
        else
            Positions[i] = Positions[i + 1] + (Positions[i] - Positions[i + 1]).normalized * BonesLength[i];
    }

    // Forward Reaching
    for (int i = 1; i < Positions.Length; i++)
        Positions[i] = Positions[i - 1] + (Positions[i] - Positions[i - 1]).normalized * BonesLength[i - 1];

    if ((Positions[Positions.Length - 1] - targetPosition).sqrMagnitude < Delta * Delta)
        break;
}

以迭代次数和距离阈值为约束条件进行迭代，BR是从叶节点到根节点，求得子节点关节和当前结点关节的方向向量，并以子节点关节为起点移动当前骨骼，FR类似，从根节点到叶节点

骨链相对轴的移动

if (Pole != null)
{
    var polePosition = GetPositionRootSpace(Pole);
    for (int i = 1; i < Positions.Length - 1; i++)
    {
        var plane = new Plane(Positions[i + 1] - Positions[i - 1], Positions[i - 1]);
        var projectedPole = plane.ClosestPointOnPlane(polePosition);
        var projectedBone = plane.ClosestPointOnPlane(Positions[i]);
        var angle = Vector3.SignedAngle(projectedBone - Positions[i - 1], projectedPole - Positions[i - 1], plane.normal);
        Positions[i] = Quaternion.AngleAxis(angle, plane.normal) * (Positions[i] - Positions[i - 1]) + Positions[i - 1];
    }
}

设置骨骼位置和旋转

for (int i = 0; i < Positions.Length; i++)
{
    if (i == Positions.Length - 1)
        SetRotationRootSpace(Bones[i], Quaternion.Inverse(targetRotation) * StartRotationTarget * Quaternion.Inverse(StartRotationBone[i]));
    else
        SetRotationRootSpace(Bones[i], Quaternion.FromToRotation(StartDirectionSucc[i], Positions[i + 1] - Positions[i]) * Quaternion.Inverse(StartRotationBone[i]));
    SetPositionRootSpace(Bones[i], Positions[i]);
}

如果是叶节点，传入的目标方向为当前targetRotation取逆 * 开始时的targetRotation * 开始时该骨骼Rotation取逆

如果是其他节点，传入的目标方向为之前计算的开始时方向向量为起点，子关节-当前关节的向量为终点计算出的四元数 * 开始时该骨骼Rotation取逆

最后设置骨骼位置完成各个骨骼的移动

完结撒花~

pid:62361510

Unity

#算法

FABIK算法

https://baifabaiquan.cn/2023/03/27/反向动力学FABRIK/

作者

白发败犬

发布于

2023年3月27日

许可协议

WX Miniprogram XR System 上一篇

Unity TimerManager 下一篇